A Python Package to Generate Synthetic Data: SDV – Example with Gaussian Copula
Creating synthetic data is becoming more and more important due to privacy issues or many other reasons. Synthetic data are expected to de-identify individuals while preserving the distributional properties of the data. I am going to introduce a Python package: SDV. SDV package includes various methods to generate synthetic data such as copulas and deep learning algorithms. You can generate synthetic data for relational databases as well. See sdv.dev web page for documentations.
I will show an example of a multivariate copula today. I am downloading a data set used in David Card’s famous return to schooling paper. Card estimates the return to schooling using 2-Stage Least Squares. I am going to create a synthetic data set for some of the selected variables. Afterward, I will evaluate the quality of the synthetic data. Let’s get the data:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from copulas.multivariate import GaussianMultivariate
from statsmodels.regression.linear_model import OLS
from stargazer.stargazer import Stargazerdf = pd.read_stata('http://fmwww.bc.edu/ec-p/data/wooldridge/card.dta')For simplicity, I am going to fill missing values with median.
df = df.fillna(df.median())I would like to use variables used in 1st stage estimations of 2SLS (but excluded some variables). I will regress education on some exogenous variables. Here is the list of variables:
X = ['married', 'exper', 'expersq',
'nearc2', 'nearc4', 'fatheduc', 'motheduc',
'weight', 'black', 'smsa', 'south', 'IQ']
Y = ['educ']
all_X = X+YI use the Gaussian Multivariate Copula to create synthetic data:
s_df = GaussianMultivariate()
s_df.fit(df[all_X])C:\Users\alfur\Miniconda3\lib\site-packages\scipy\stats\_continuous_distns.py:4798: RuntimeWarning: divide by zero encountered in true_divide
return c**2 / (c**2 - n**2)
C:\Users\alfur\Miniconda3\lib\site-packages\scipy\stats\_distn_infrastructure.py:2407: RuntimeWarning: invalid value encountered in double_scalars
Lhat = muhat - Shat*mu
C:\Users\alfur\Miniconda3\lib\site-packages\scipy\stats\_continuous_distns.py:4789: RuntimeWarning: divide by zero encountered in power
return cd2*x**(c-1)
C:\Users\alfur\Miniconda3\lib\site-packages\scipy\stats\_continuous_distns.py:5756: RuntimeWarning: overflow encountered in true_divide
lPx -= 0.5*np.log(r*np.pi) + (r+1)/2*np.log(1+(x**2)/r)
C:\Users\alfur\Miniconda3\lib\site-packages\scipy\stats\_continuous_distns.py:5756: RuntimeWarning: overflow encountered in square
lPx -= 0.5*np.log(r*np.pi) + (r+1)/2*np.log(1+(x**2)/r)
C:\Users\alfur\Miniconda3\lib\site-packages\copulas\univariate\truncated_gaussian.py:43: RuntimeWarning: invalid value encountered in double_scalars
a = (self.min - loc) / scale
C:\Users\alfur\Miniconda3\lib\site-packages\copulas\univariate\truncated_gaussian.py:44: RuntimeWarning: divide by zero encountered in double_scalars
b = (self.max - loc) / scale
C:\Users\alfur\Miniconda3\lib\site-packages\scipy\optimize\slsqp.py:63: RuntimeWarning: invalid value encountered in subtract
jac[i] = (func(*((x0+dx,)+args)) - f0)/epsilon
C:\Users\alfur\Miniconda3\lib\site-packages\scipy\stats\_continuous_distns.py:547: RuntimeWarning: invalid value encountered in sqrt
sk = 2*(b-a)*np.sqrt(a + b + 1) / (a + b + 2) / np.sqrt(a*b)
C:\Users\alfur\Miniconda3\lib\site-packages\scipy\optimize\minpack.py:162: RuntimeWarning: The iteration is not making good progress, as measured by the
improvement from the last ten iterations.
warnings.warn(msg, RuntimeWarning)
C:\Users\alfur\Miniconda3\lib\site-packages\copulas\univariate\truncated_gaussian.py:43: RuntimeWarning: divide by zero encountered in double_scalars
a = (self.min - loc) / scale
C:\Users\alfur\Miniconda3\lib\site-packages\copulas\univariate\truncated_gaussian.py:44: RuntimeWarning: invalid value encountered in double_scalars
b = (self.max - loc) / scale
C:\Users\alfur\Miniconda3\lib\site-packages\scipy\optimize\minpack.py:162: RuntimeWarning: The iteration is not making good progress, as measured by the
improvement from the last five Jacobian evaluations.
warnings.warn(msg, RuntimeWarning)I draw sample from my Gaussian Copula with the same size of my data:
s_data = s_df.sample(len(df))Let’s compare two datasets with basic summary statistics:
df[all_X].describe().transpose().round(2)| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| married | 3010.0 | 2.27 | 2.07 | 1.0 | 1.0 | 1.0 | 4.0 | 6.0 |
| exper | 3010.0 | 8.86 | 4.14 | 0.0 | 6.0 | 8.0 | 11.0 | 23.0 |
| expersq | 3010.0 | 95.58 | 84.62 | 0.0 | 36.0 | 64.0 | 121.0 | 529.0 |
| nearc2 | 3010.0 | 0.44 | 0.50 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 |
| nearc4 | 3010.0 | 0.68 | 0.47 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| fatheduc | 3010.0 | 10.00 | 3.27 | 0.0 | 8.0 | 10.0 | 12.0 | 18.0 |
| motheduc | 3010.0 | 10.54 | 3.03 | 0.0 | 9.0 | 12.0 | 12.0 | 18.0 |
| weight | 3010.0 | 321185.25 | 170645.80 | 75607.0 | 122798.0 | 365200.0 | 406024.0 | 1752340.0 |
| black | 3010.0 | 0.23 | 0.42 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| smsa | 3010.0 | 0.71 | 0.45 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| south | 3010.0 | 0.40 | 0.49 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 |
| IQ | 3010.0 | 102.62 | 12.76 | 50.0 | 98.0 | 103.0 | 108.0 | 149.0 |
| educ | 3010.0 | 13.26 | 2.68 | 1.0 | 12.0 | 13.0 | 16.0 | 18.0 |
s_data[all_X].describe().transpose().round(2)| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| married | 3010.0 | 2.30 | 2.13 | -0.52 | 0.84 | 1.23 | 4.19 | 7.62 |
| exper | 3010.0 | 8.83 | 4.25 | -1.14 | 5.90 | 8.20 | 11.39 | 25.02 |
| expersq | 3010.0 | 95.54 | 88.27 | -38.26 | 34.08 | 68.51 | 129.27 | 568.98 |
| nearc2 | 3010.0 | 0.44 | 0.51 | -0.35 | -0.01 | 0.13 | 0.98 | 1.32 |
| nearc4 | 3010.0 | 0.69 | 0.48 | -0.27 | 0.07 | 0.95 | 1.03 | 1.37 |
| fatheduc | 3010.0 | 10.02 | 3.21 | -1.42 | 8.32 | 10.23 | 11.91 | 19.85 |
| motheduc | 3010.0 | 10.61 | 3.01 | -0.24 | 8.72 | 11.44 | 12.30 | 18.92 |
| weight | 3010.0 | 318721.50 | 167928.40 | -6296.75 | 138158.44 | 358169.97 | 418018.70 | 1422281.72 |
| black | 3010.0 | 0.23 | 0.42 | -0.31 | -0.04 | 0.03 | 0.16 | 1.26 |
| smsa | 3010.0 | 0.71 | 0.46 | -0.28 | 0.11 | 0.95 | 1.03 | 1.30 |
| south | 3010.0 | 0.39 | 0.50 | -0.32 | -0.02 | 0.09 | 0.96 | 1.33 |
| IQ | 3010.0 | 102.77 | 12.85 | 48.59 | 97.98 | 103.10 | 108.55 | 149.97 |
| educ | 3010.0 | 13.03 | 2.46 | 3.68 | 11.36 | 13.16 | 14.87 | 17.97 |
Immediately, we find two problems related with the Gaussian Copula: (1) Dummary variables are not recognized. The could become less than 0 or greater than 1. (2) integer variables are not recognized and impossible values appears. For example, experience variable cannot be less than 0.
This is not surprising. Let’s compare distribution of some variables on 3D plots:
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(1,2,1,projection='3d')
ax1.scatter(df.educ, df.exper, df.IQ)
ax2 = fig.add_subplot(1,2,2,projection='3d')
ax2.scatter(s_data.educ, s_data.exper, s_data.IQ)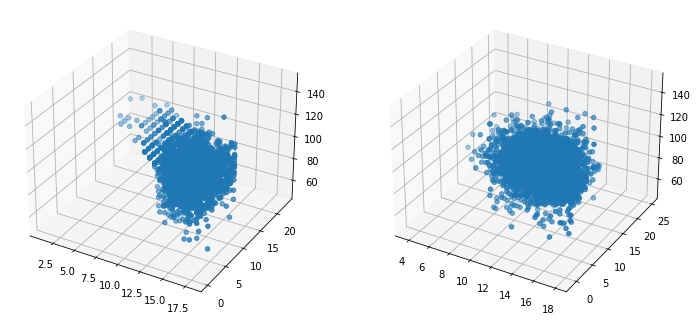
The education variable is a discrete variable. We see that the Gaussian copula turns it into a continuous variable just like others. It looks like chaos on the right-hand side! I would like to investigate whether distributional properties are preserved or not.
As distribution assumed to be Gaussion, covariance matrices are very similar:
df[all_X].cov().round(2).iloc[1:8,1:8]| exper | expersq | nearc2 | nearc4 | fatheduc | motheduc | weight | |
|---|---|---|---|---|---|---|---|
| exper | 17.15 | 338.97 | -0.01 | -0.12 | -4.12 | -3.31 | -1.847862e+04 |
| expersq | 338.97 | 7160.26 | -0.24 | -2.52 | -78.35 | -64.72 | -5.315395e+05 |
| nearc2 | -0.01 | -0.24 | 0.25 | 0.03 | 0.14 | 0.09 | 1.989730e+03 |
| nearc4 | -0.12 | -2.52 | 0.03 | 0.22 | 0.19 | 0.10 | 7.425300e+03 |
| fatheduc | -4.12 | -78.35 | 0.14 | 0.19 | 10.67 | 5.18 | 1.138799e+05 |
| motheduc | -3.31 | -64.72 | 0.09 | 0.10 | 5.18 | 9.21 | 1.064642e+05 |
| weight | -18478.62 | -531539.47 | 1989.73 | 7425.30 | 113879.94 | 106464.16 | 2.911999e+10 |
s_data[all_X].cov().round(2).iloc[1:8,1:8]| exper | expersq | nearc2 | nearc4 | fatheduc | motheduc | weight | |
|---|---|---|---|---|---|---|---|
| exper | 18.04 | 362.92 | -0.08 | -0.14 | -4.18 | -3.47 | 3.414371e+04 |
| expersq | 362.92 | 7791.49 | -1.81 | -3.26 | -81.23 | -68.28 | 6.499460e+05 |
| nearc2 | -0.08 | -1.81 | 0.26 | 0.03 | 0.11 | 0.04 | 6.308000e+01 |
| nearc4 | -0.14 | -3.26 | 0.03 | 0.23 | 0.16 | 0.10 | 8.522730e+03 |
| fatheduc | -4.18 | -81.23 | 0.11 | 0.16 | 10.27 | 4.98 | 9.190515e+04 |
| motheduc | -3.47 | -68.28 | 0.04 | 0.10 | 4.98 | 9.03 | 8.162761e+04 |
| weight | 34143.71 | 649945.98 | 63.08 | 8522.73 | 91905.15 | 81627.61 | 2.819995e+10 |
I am more interested in linear regression results:
fit1 = OLS(df[Y], df[X]).fit()
fit2 = OLS(s_data[Y], s_data[X]).fit()
Stargazer([fit1, fit2])| Dependent variable:educ | ||
| (1) | (2) | |
| IQ | 0.087*** | 0.091*** |
| (0.002) | (0.002) | |
| black | 0.575*** | 0.582*** |
| (0.114) | (0.106) | |
| exper | 0.151*** | -0.023 |
| (0.031) | (0.033) | |
| expersq | -0.020*** | -0.006*** |
| (0.002) | (0.002) | |
| fatheduc | 0.135*** | 0.089*** |
| (0.014) | (0.015) | |
| married | -0.004 | 0.007 |
| (0.019) | (0.019) | |
| motheduc | 0.175*** | 0.210*** |
| (0.014) | (0.015) | |
| nearc2 | 0.086 | 0.229*** |
| (0.077) | (0.078) | |
| nearc4 | 0.439*** | 0.340*** |
| (0.087) | (0.087) | |
| smsa | 0.406*** | 0.242*** |
| (0.090) | (0.089) | |
| south | 0.251*** | 0.189** |
| (0.083) | (0.083) | |
| weight | 0.000*** | 0.000*** |
| (0.000) | (0.000) | |
| Observations | 3,010 | 3,010 |
| R2 | 0.977 | 0.974 |
| Adjusted R2 | 0.977 | 0.974 |
| Residual Std. Error | 2.039 (df=3002) | 2.132 (df=2998) |
| F Statistic | 16193.365*** (df=8; 3002) | 9452.387*** (df=12; 2998) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
|
I could tell that it performs way more better than I expected. I believe one could generate much more better synthetic data with deep learning algorithm.

