Inductive vs. Deductive Reasoning – Examples

This course aims to explain inductive reasoning and its reflection on our daily life. However, induction is only one aspect of reasoning. We will discuss deductive reasoning in this article and compare it with induction.

Definition: Deduction

Let’s consult our holy source, Wikipedia. Or not? Because it has a terrible page for deductive reasoning. To be honest, I am surprised (The inductive reasoning page in Wikipedia is well prepared.). Nevertheless, it has one paragraph on Sherlock and how he popularized deductive reasoning.

Got the definition from Oxford dictionary:

The inference of particular instances by reference to a general law or principle.

Oxford Dictionary

It is clear from the definition that deduction is based on general law or principle. Or information… In practice, we produce hypotheses and test them with inductive reasoning.

Now, recall the definition of induction: a method of reasoning in which the premises are viewed as supplying some evidence, but not full assurance, of the truth of the conclusion. So, inductive reasoning produces information (Generalizations/theories), and deductive reasoning tests the hypotheses. The following image explains the cycle:

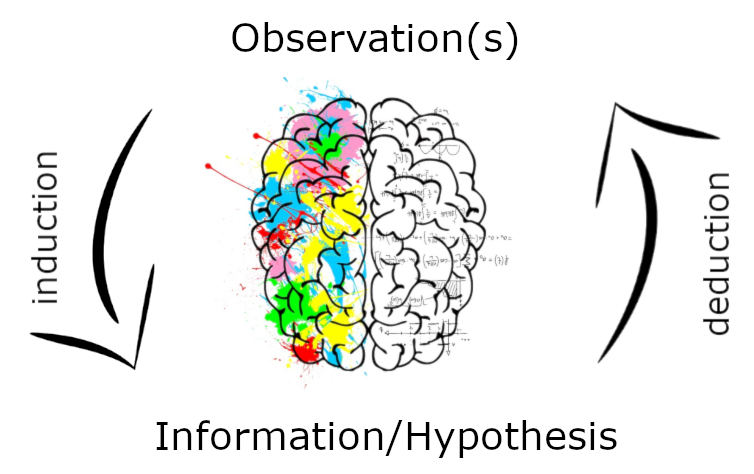
Examples

Some examples for deduction.

Theory: If the sum of digits of a number is divisible by 3, then the number is divisible by 3 as well.
Premise: Digits of 471 sums to 4+7+1=12.
Conclusion: 471 is divisible by 3 because 12 is divisible by 3.

Theory: All noble gases are stable.
Premise: Helium is a noble gas.
Conclusion: Helium is stable.

Deduction could be probabilistic as well.

Theory: 90% of Turkish people have black hair.
Premise: Eren is from Turkey.
Conclusion: Eren has black hair with 0.9 probability.

Let’s go back to the first example and try to induce the theory:

Observation 1: 12 is divisible by 3 and 1+2=3 is divisible by 3 as well.
Observation 2: 42 is divisible by 3 and 4+2=6 is divisible by 3 as well.
Observation 3: 126 is divisible by 3 and 1+2+6=9 is divisible by 3 as well.
Observation 4: 375 is divisible by 3 and 3+7+5=15 is divisible by 3 as well.
…
Conclusion: If the sum of digits of a number is divisible by 3, then the number is divisible by 3 as well.

Do you see the problem with this reasoning? There are infinite possible observations. So how can we make sure that our conclusion is correct? (This is why we say “not full assurance” in the definition of inductive reasoning.)

First of all, such a method is very useful to create theories, but it must be confirmed that it is True. We usually use deductive methods (e.g., Proof by Contradiction) to prove that conclusion is correct. So, the validity of inductive reasoning often requires the confirmation of deduction.

Daily Life Reasoning

If you, for instance, think about chess, you will see that players mostly use “deduction.” It is not about producing theories or hypotheses. There are rules, and we try to win by rules. We memorized some openings, or maybe we enjoy specific moves. But we do not produce theories (mostly). This is another reason why chess-like strategic thinking does not reflect real life. Real-life requires us to be creative, social, and have other types of soft skills. Soft skills often cannot be acquired from textbooks. We develop such skills by observing ourselves and others. If we can use the deduction-induction cycle efficiently, we will have an “accurate” understanding of the world and will be able to respond to changes (e.g., crisis) effectively.

While inductive reasoning is used to understand the real-life mechanics, it could also be “toxic” if not collaborated with an effective deduction (a filter). People tend to generalize their experiences (Often only one observation) and shape their worldview accordingly. Full of nonfiltered and contradictive opinions… It is very easy to fall into this trap because reasoning is not effortless. In fact, because our brain is the number-one energy consumer organ in our body, the reasoning is very costly. Hence, our brain “saves energy” with such shortcuts. Looking for observations to make a conclusion, testing theories, and looking for alternative explanations require a lot of effort.

How can I improve my logical reasoning? I reply to people, “Learn basic principles of logical reasoning, and, then, more carefully observe yourself.” It means to review your political opinions, try to understand your relations (with family, friends, etc.), spare more time/effort when you criticize (someone or an opinion), question your career choices, and so on. Once one starts, he/she will understand that it requires immense effort. Also, I do not know of any better training. It is a life-long learning process.